一些不知道放哪,但是需要注意的问题
反函数与复合函数
对于函数
同时,反函数具备与原函数相同的单调性
积分比较大小
这类题目考的比较常见。
比较大小一般有两种方法,一种是直接将这个积分计算出来,对积分值进行比较。另外一种是相减,判断大于还是小于
如果遇到
无限延长(循环)曲线求体积
首先要看定义域,比较常见的有:
因为定义域改变了,所以其积分上下限就变了。
但是此时的积分上下限还是带有
积分中出现极限
当积分中出现极限的时候,要先将极限计算出来,将极限给去掉,当然这个时候要注意积分的上下限问题。
同时,还要注意正、负问题。
求极限(二元函数)出现震荡函数
当在求极限的时候遇到
例如:
在判断其连续的时候,要考虑使用夹逼准则。
所以直接去掉不用管。
通过夹逼得到:
进而得到从极限为
在多元函数中判断 f 仅为 b 和 c 的函数
这种类型的题目不多,但是有。
直接用例题来说明:
1800 P 92 T 13
设
若
解:
只需要证明
上面第二行其实是将其反带入,将求导得到
这种题目一般都需要取巧
多元函数在一次函数形式下的判断
IMPORTANT
有的时候,当题目中没有明确说明
例 880 P 43 T 9
在已知一阶导的情况下求二阶导
除了可以使用求导计算的时候,针对抽象导数使用下面的方法:
已知
则:
前面即使有系数也无所谓。
多元函数下求原函数
大部分都是二元函数下求解。
一般可以使用积分一步步推导出来。
有时候当出现微分方程形式的时候(二阶线性或者非线性),需要使用解微分方程的方法来计算。
函数奇偶性判断
复合函数判断
| 条件 | 结论 | 解释 |
|---|---|---|
| 奇函数 | ||
| 偶函数 | ||
| 偶函数 | ||
| 不一定 | 一般不能判断奇偶性,需具体代入 |
函数相乘判断
| 偶 | 偶 | 偶 |
| 奇 | 奇 | 偶 |
| 奇 | 偶 | 奇 |
| 偶 | 奇 | 奇 |
| 任意 | 非奇非偶 | 非奇非偶 |
| 非奇非偶 | 非奇非偶 | 不一定 |
反三角函数与三角函数的复合函数
先正后反
只有当
其值为:
其值域为
其值为:
只有当
其值为:
先反后正:
这个相对来说比较常见。
当
当
当
大部分情况都是在
当
当
当
当
当
二重积分下求体积
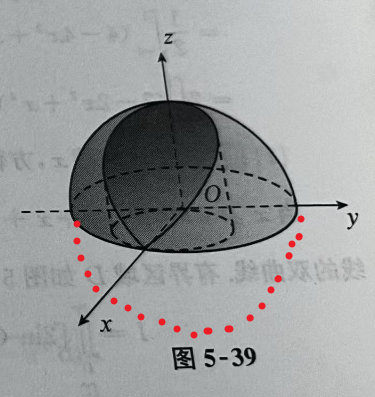
这类题目的特点是一般说求某平面图形在一立体图形上截取部分的体积。
IMPORTANT
一般被截取的图形的函数为:
一般设为
同时,在计算的时候,要注意奇偶性与对称性。因为大部分都是对称的,可以简化计算。
函数中包含积分并求此函数问题
无论是在一重积分还是在二重积分中,此类问题都有出现。
下面以一个二重积分为例:
880 P 52 T (14)
设
求
方法就是设
然后对等式两边分别求积分:
那么就可以得到:
然后计算出上面的积分即可,其中
一重积分同理。
不等式中包含积分(不等式与导数)
当遇到不等式的时候,应该考虑结合起来利用导数来求解。
NOTE
当不等式中包含积分的时候,求解方法依然是结合起来构成大
在构造大
通过微分方程求原函数
与直接解微分方程不一样,主要是与其他知识点结合,比如在含有变限积分的方程(如下面的方程)中求原函数
这部分应该与上面的“不等式中包含积分”结合起来看待。
求原函数问题
此类问题一般有:
- 积分求解
- 导数定义反解
- 微分方程
甚至于说,很大的概率会将这几个部分结合起来。
NOTE
当某些函数如果满足:对任意
快速抓大头
抓大头直接得到结果:
例题:
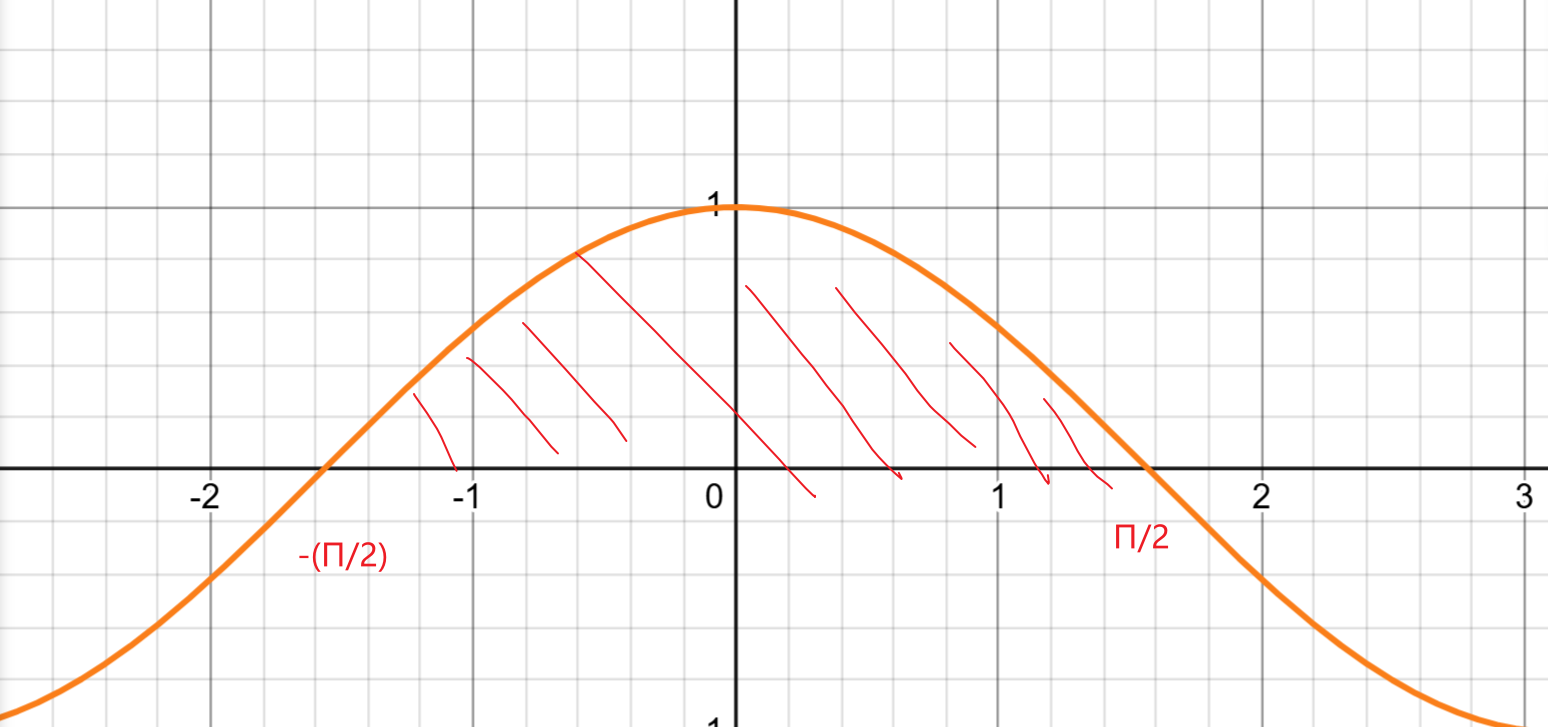
这个函数的图像如下:
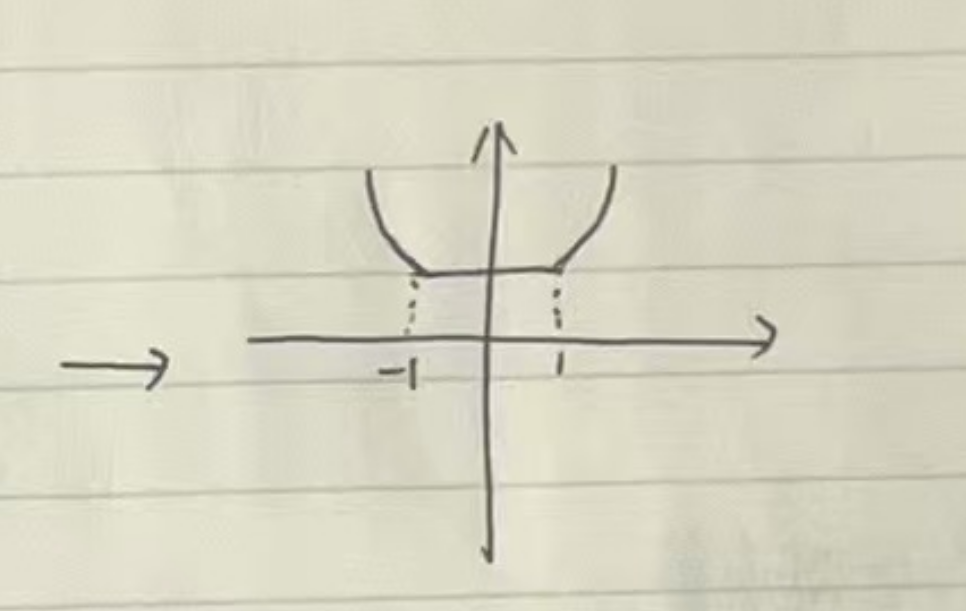
可以很轻松的得到
指数相乘三角函数的快速求积分
这个是对于指数相乘三角函数的快速求积分的方法
需要注意的是,核心是计算这个行列式。
需要记忆这个函数的图像。

记忆
的有关性质。
1、
2、
3、
这个公式的推导来自于基本积分公式:
4、
等价无穷小,这个有时候用的挺多的
一般只用到前两项,如果还有必要,做题遇到再说,因为这个函数的导数不是很好求,不过依然可以用泰勒展开求解。
关于
1、
2、
3、
4、
导数与原式同时出现
如果
第一个,考虑拉格朗日中值定理
第二个,考虑积分
积分、连续、可导之间的关系
连续不一定可导,可导一定连续
不连续一定不可导
设
换句话说,如果能都能写出积分公式,则一定可积。而
例如:
设
因为已经写出了积分公式,所以其肯定是连续的,而在
直接就可以得到:
现在还有一种经常出现问题的结论:
但凡涉及到在某个点处(在某个点的邻域内)的导数大于
NOTE
只要是涉及到某个点处(或者某个点的邻域内)的问题,都要格外注意。
导数与极值的问题
IMPORTANT
若
若
若
IMPORTANT
反过来说,若
其中,当二阶导数小于 0(
二阶导数大于 0(
IMPORTANT
若
参数方程求导
反函数求导问题
然后是反函数:
一阶导:
二阶导:
常见导数中的构造问题
做差
无论是在高考还是考研中,都很难处理两个函数的问题,比如
一般都要转换成一个函数来处理。
方法一般为做差
导数与原函数之间的构造问题
一般来说,只要题目中提供了导数与原函数之间的等数关系
那么接下来就是要考虑使用构造函数的公式:
若欲证结论为"
其他常见的构造函数
比如遇到
比如遇到
常见函数的极限
例题:
这里需要分左右极限来处理。
全微分方程
其中
反常积分的敛散性
当
, 的时候收敛
当 1.
当
当
当
三步走和四步走
对于
可以得到:
核心在于将
对于
可以得到:
关键是在于要学会对
三角函数与反三角函数以及导数
首先是三角函数:
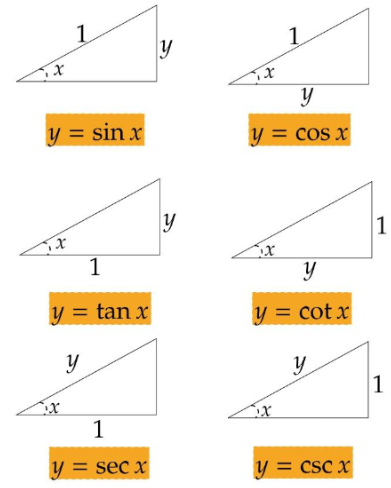
三角函数求导不再赘述,至于后面复杂的三角函数,之间换回到简单三角函数即可。
然后是反三角函数:
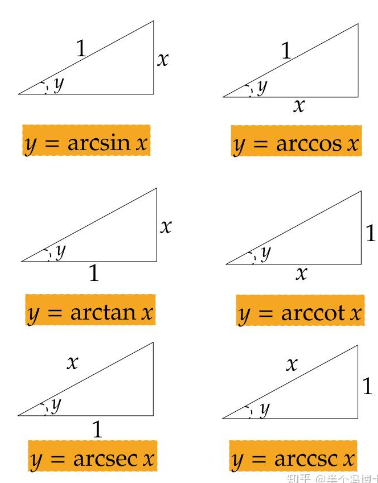
反三角函数的求导在下面:

三角恒等变换相关公式
积化和差以及和差化积公式
记忆口诀: 正加正,正在前, 余加余,余并肩。 正减正,余在前, 余减余,负正弦。
积化和差公式:
记忆口诀: 积化和差得和差, 余弦在后要相加; 异名函数取正弦, 正弦相乘取负号。
和差角公式
六边形关系
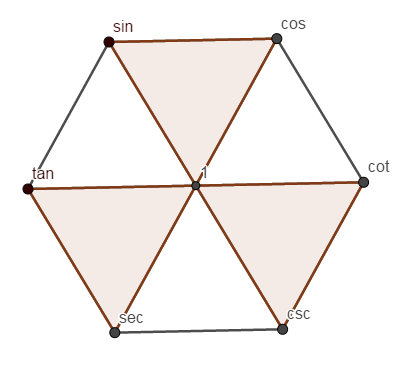
其中有三组关系:
- 边上的三角函数两边相乘等于中间
- 染了色的三角形上面两个三角函数的平方和等于下面的
- 相对的三角函数是倒数关系
二倍角公式
三倍角公式
半角公式
注意,具体需要符号看象限
降幂公式
辅助角公式
其中,
点鞭炮公式
万能公式
辅助记忆图:
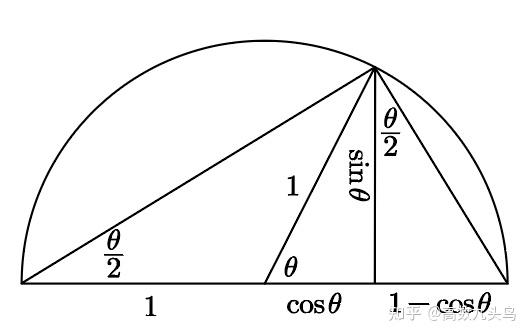
切线方程
过
若过P另有曲线C的切线,切点为
曲率与曲率半径
曲率,主要是用到了与导数相关的知识。
曲率:
曲率半径:
曲线渐近线问题
曲线的斜渐近线
上面公式中的
曲线的水平渐近线
当
曲线的垂直渐近线
渐进线的极限存在问题
直接上例题:
设
主要看,在上面的这个极限中,极限值是存在的,但是很明显,当
那么变换一下就可以得到:
所以
IMPORTANT
注意,斜渐近线一定是斜着的
中值定理
罗尔中值定理
若
拉格朗日中值定理
若
柯西中值定理
- 若
都在 上连续,都在 上可导,且 ,则至少存在一点 . 使 - 当
时 : 柯西 拉格朗日
泰勒中值定理
如果函数
积分中值定理
设函数
中值定理的构造问题
若欲证结论为"
设向量组
二重积分中值定理
欧拉公式
泰勒公式的一些应用
首当其冲的就是求极限
这个就不多讲了,不过需要注意的是,一般上来讲,是
其次,就是泰勒公式与高阶导数之间的关系
这里不再赘述。
这里主要是说明泰勒公式在求和方面的应用。(或许未来会整理到一个单独的文件中。)
注意到常见的泰勒展开式前面是有系数的。
也就是说,当涉及到"系数"相加的情况,可以考虑泰勒公式。
例如下面这两个例子:
这里主要用到了
令
另外一个例子:
这个是用到了
当
以此类推,可能会有
一些积分相关的东西
基本积分公式
下面补充积分:
下面这俩个积分如果不背下来的话,也可以考虑分部积分法来构成循环积分来求解。
比较常用的三角变换:
积分中含有根号的问题
首先考虑上面的三角变换,变换到基本积分公式(看上面即可)
然后是考虑图像,有时候针对根号下积分的问题用圆或者椭圆的面积来解决
考虑直接令根号下全部等于
,进行换元计算,也是凑微分的一种方法 其他待补充
变上限积分
变上限积分的无穷小问题
例题:
根据上面的公式,得到原式是
变上限积分求导问题
此外,注意换元问题。如果是被积函数的主体是一个抽象函数,例如:
奇函数积分与偶函数积分
IMPORTANT
在对称区间上,对奇函数求积分得到的结果为
柯西积分不等式
若
形如
核心要义就是令分子 = A 分母+B 分母的导数
例如:
令
可有得到:
通过解方程,我们可以把
然后,就可以直接得到结果:
其实就是设分母为
则分子是:
就可以得到:
贝塔函数和伽马函数
贝塔函数
贝塔函数的定义是:
贝塔函数性质
对称性:
特殊值:
与伽马函数之间的关系
用这个可以快速求积分。
伽马函数
伽马函数的定义如下:
其中,伽马函数具备以下这样的递推关系:
特别的是:
除此之外,伽马函数还有以下性质:
半整数阶公式:
定积分求体积
些许题目的可以使用传统的求体积的方法:
贴近 x 轴 y 轴求体积
绕 x 轴旋转一周:
绕 y 轴旋转一周:
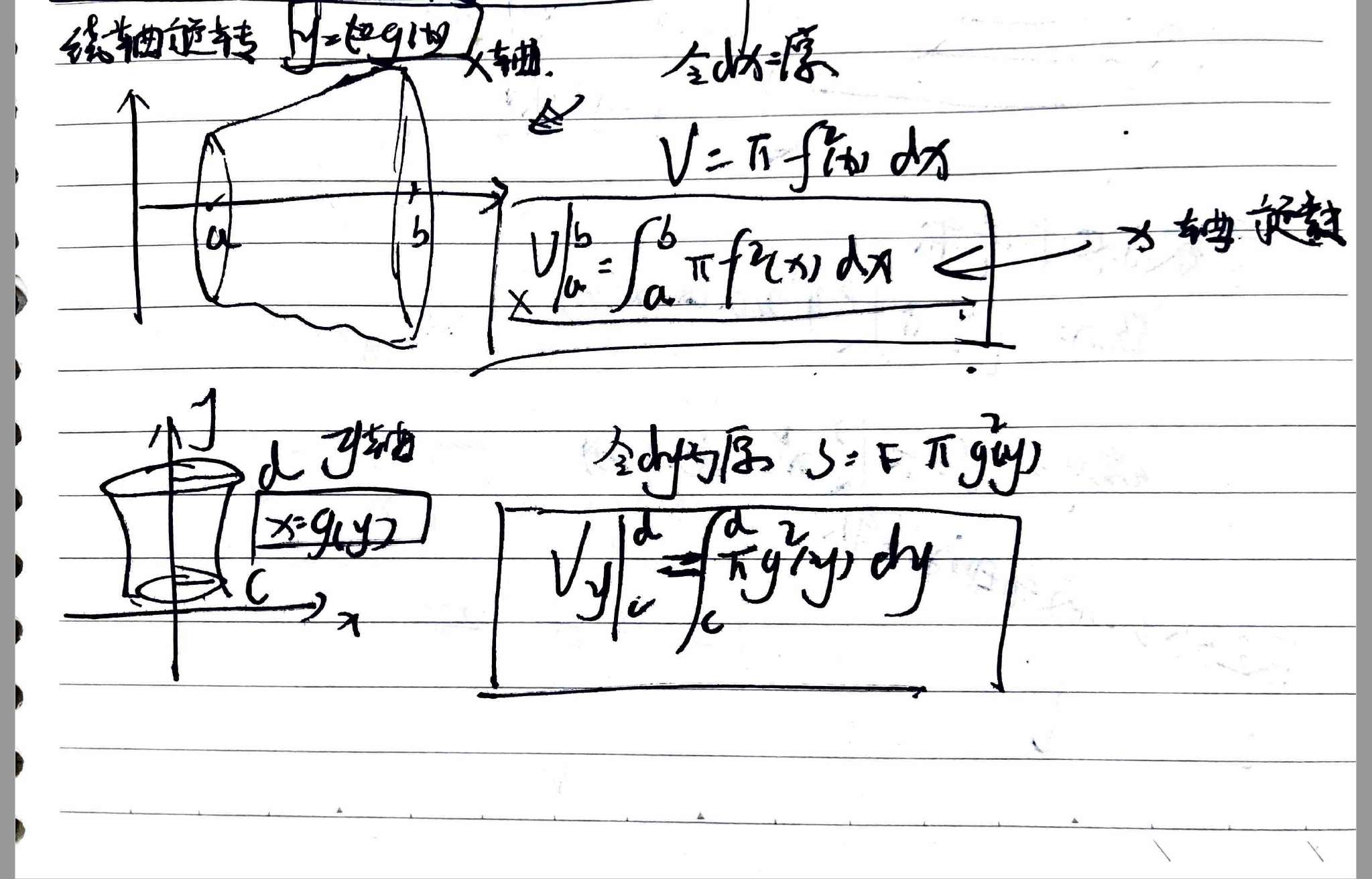
上面的公式适用于旋转体与 x 轴或 y 轴相近的情况,如果出现不相接触的情况用下面这个公式:
不贴近 x 轴 y 轴求体积
绕 y 轴:
绕 x 轴:
IMPORTANT
注意,上面绕 x 轴公式中的
参数方程求体积
直接上方程
绕 x 轴:
绕 y 轴:
极坐标绕极轴的体积
除极坐标的通用方法
利用二重积分求解定积分体积问题。
任意图形绕任意轴旋转一周的体积,有公式:
其中
直线距离公式 #点到直线距离公式 :设直线方程为
用语言描述就是,将这个点代入到这个方程中,然后除以方程系数平方和的开根号。
这么说不太好理解,来个例题:
求
根据上面的方法,可以直接列公式:
上面就是利用二重积分求解体积。
不过需要注意的是,上面这个限制范围的
求
依然是直接列公式:
古尔丁定理(快速求体积)
平面上一区域内
NOTE
这个一般用于选择填空,大题不要用
例如下图:
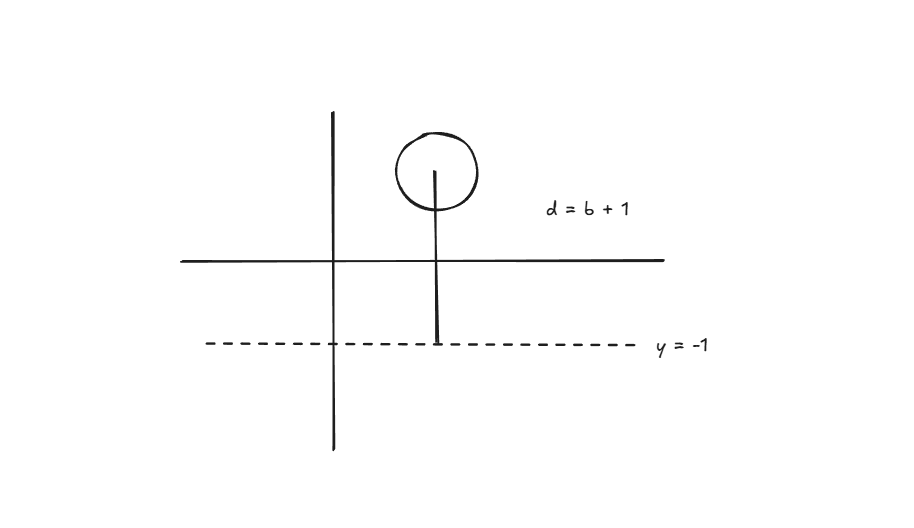
此圆绕
针对圆的一些方法
一般来说,有关于圆绕某直线旋转一周得到的体积可以使用上面的古尔丁定理。
但是,对于计算过程,还是很有必要的。
尤其是圆上 一部分 的旋转体积的求法。
旋转曲面的侧面积问题
这里依然也是三种类型,分别是常见方程、参数方程、极坐标方程
通用方程:
常见方程(直角坐标)
设曲线为:
则得到:
参数方程
给出
极坐标形式
弧长问题
标准方程
对于
参数方程
对于
极坐标方程
对于
圆
圆的标准方程:
在平面直角坐标系内,以
圆的一般方程,也是在平面直角坐标系内。
其中,
圆心:
半径:
注意,若
参数方程:
圆心为
极坐标方程:
圆的半径为
圆心在极点处时候:

极坐标方程为:
圆心在极轴上的圆,半径为

极坐标方程表示为:
过极点的圆:
圆心为

极坐标方程为:
椭圆
标准方程:
当焦点在
当焦点在
以上椭圆方程的中心在原点
椭圆的面积:
其中,
椭圆的离心率:
其中,
NOTE
特别需要注意的是,椭圆的面积有可能会被用在计算其面积最大(最小)的情况下,在二元函数中常见。
解决方法是利用拉格朗日乘子法。
双曲线
这部分包括上面的椭圆,在定积分以及二重积分上用的比较多。
标准方程
焦点在
焦点坐标:
焦点在
焦点坐标:
两焦点间的距离
等轴双曲线
等轴双曲线是指实轴长等于虚轴长。
其离心率固定为
注意,一般来说,出现次数比较多的是等轴双曲线平移之后。
反比例函数
平移后的形式:
当然,还有可能是下面这个形式:
形式就是平移之后的等轴双曲线,这个需要格外注意。
四种常用曲线
经常用于定积分求面积以及二重积分求体积。
星形线
基本方程:
参数方程:
图像:
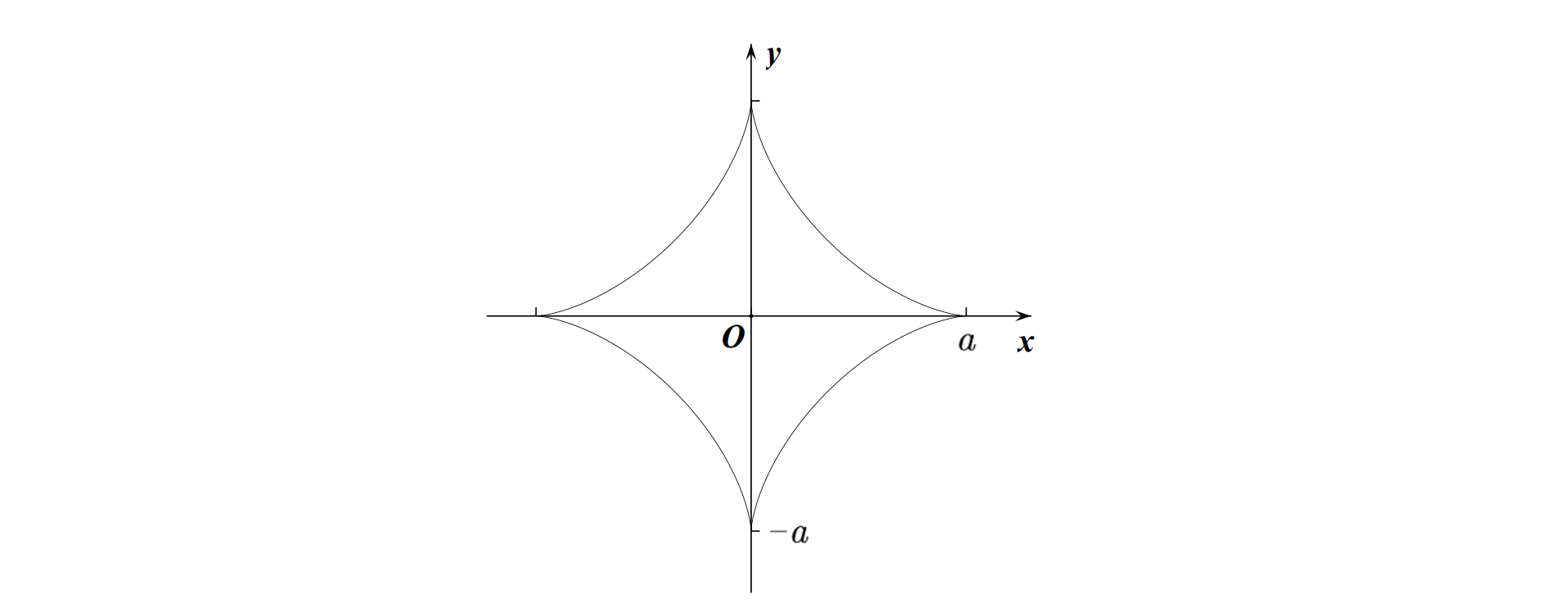
摆线
参数方程:
图像:
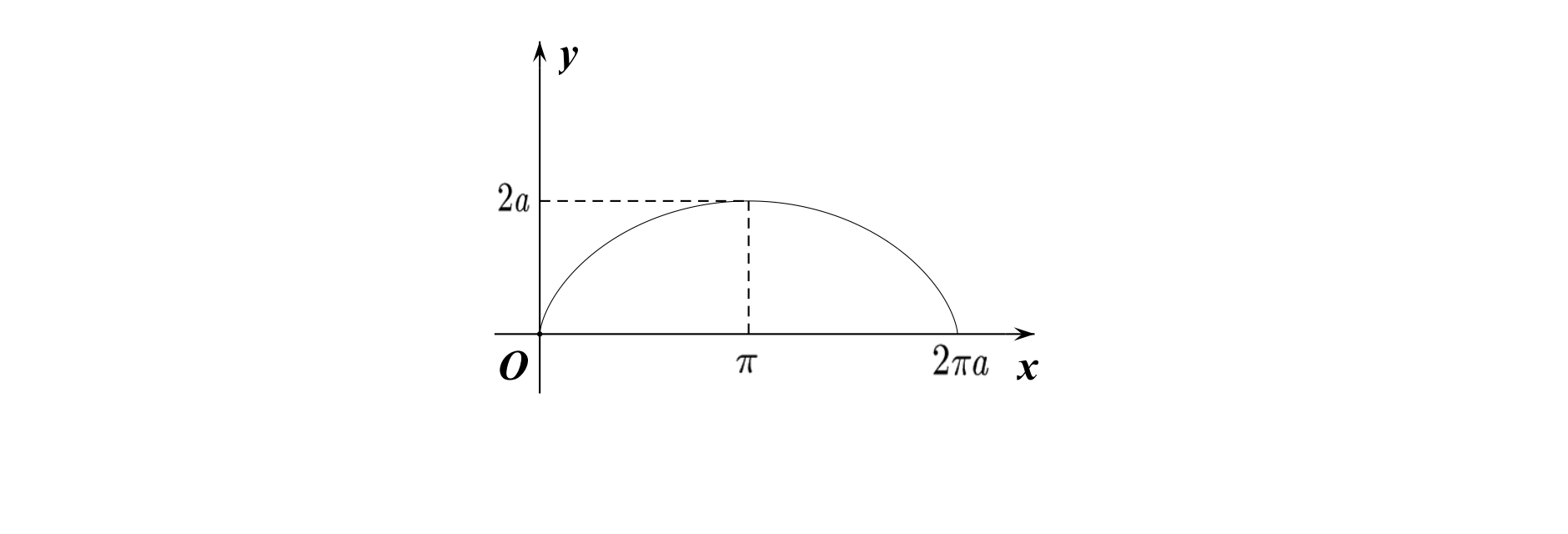
心形线
基本方程:
极坐标方程:
图像:
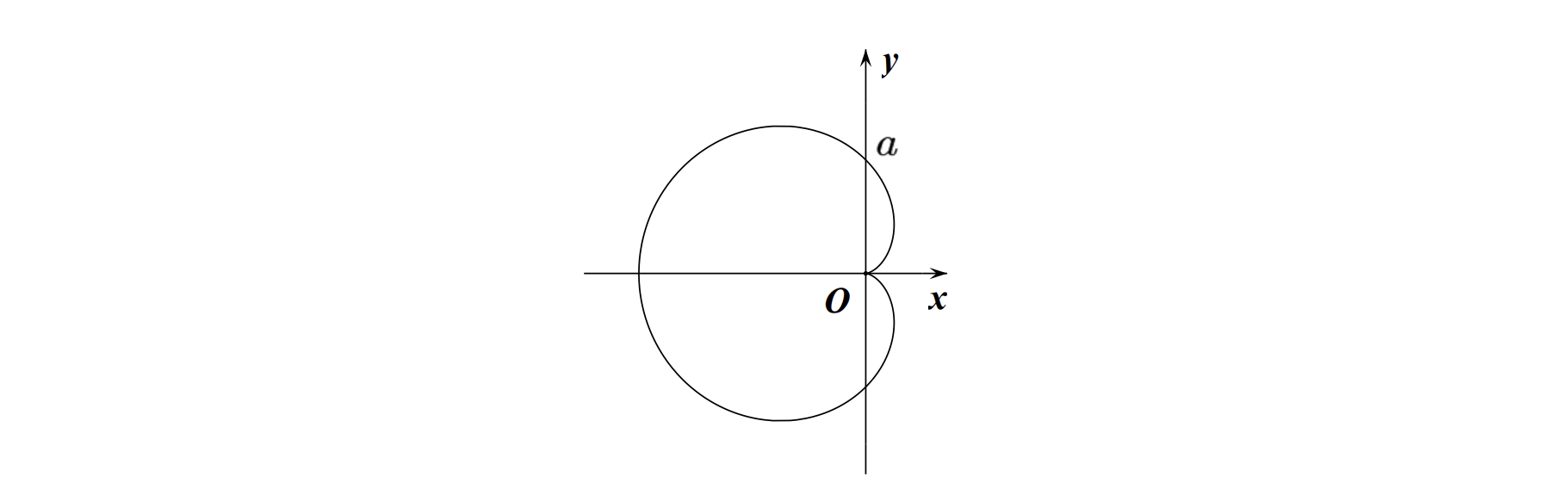
伯努利双纽线
双纽线有两个,一个关于
一般方程:
极坐标方程:
图像:
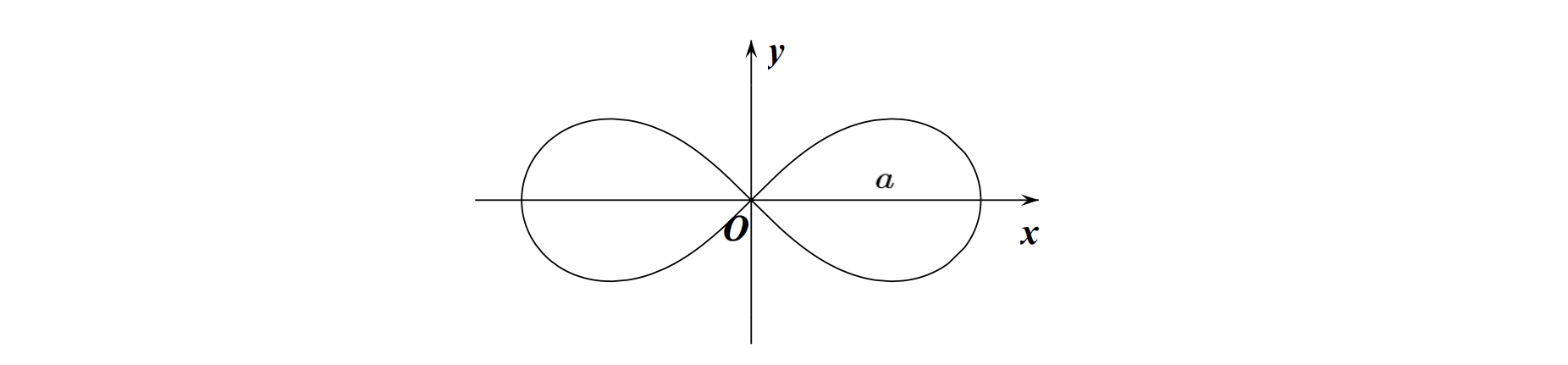
原点对称双纽线
一般方程:
极坐标方程:
图像:
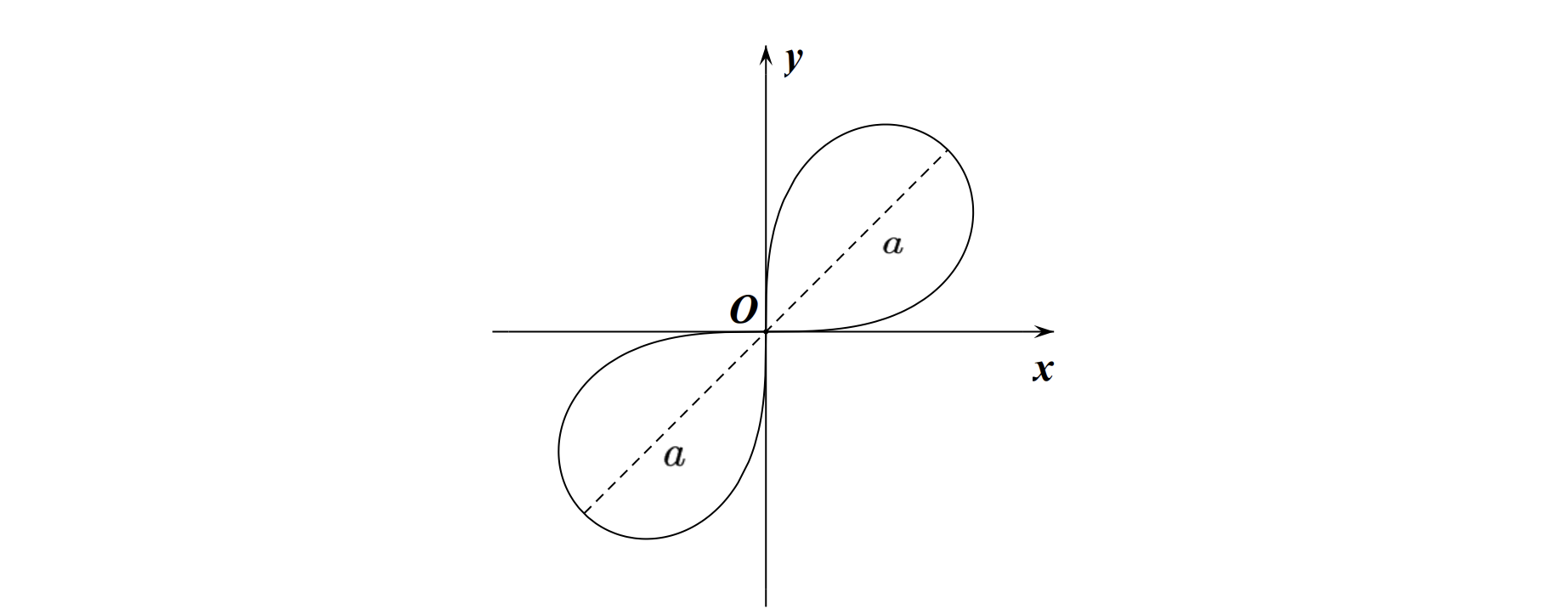
补充一个
这个经常用在二重积分上。图像如下:
需要注意的是,其关于
二重积分
坐标系转换
除直接算之外,从直角坐标系转换到极坐标系是一个很重要的方法。
注意,在变换的时候由于二重积分换元需要用雅可比矩阵进行验证
所以变换到极坐标系需要多乘一个
例如:
变量替换:
利用雅可比矩阵换元:
积分区域:
进而得到:
特别注意:
首先来看

当被积分区域为图中阴影部分时,
然后是
还是上面这个例子:
从原点出发,边界为
还有一部分是从极坐标转换为直角坐标系。
首先要看的是
这里判断的方法则是:
再根据
当然,有的时候
例如:
椭圆范围下的极坐标变换
880 P 51 T (6)
如果直接按照原来基本的方法去转换坐标系比较难算。
令
则,根据雅可比行列式计算得到:
利用这个方法更快解决问题。
二重积分的定积分定义求极限
二重积分的奇偶对称性
二重积分的奇偶性质需要结合积分区域与被积函数的奇偶性来综合判断。
当积分区域
若
当积分区域
若
NOTE
这个其实就是二重积分下面的奇零偶倍
不过,需要注意的是,在判断奇偶性的时候,需要结合积分区域和被积函数,并且这两个是相反的。
计算平面图形的形心坐标
其中:
也就是区域面积。
二重积分中的参数方程问题
这类题目比较难。
其本质是积分区域的表达形式为参数方程。
定积分与常数不等式
基本不等式
对于正实数
按照顺序得到的结果是:
调和 < 几何 < 算术 < 平方
被称为调几算方
N 元均值不等式
对于任意的正整数
写几个常用的:
在往下延申不太常用
多元函数相关问题
连续、可微、可导
三者之间的关系
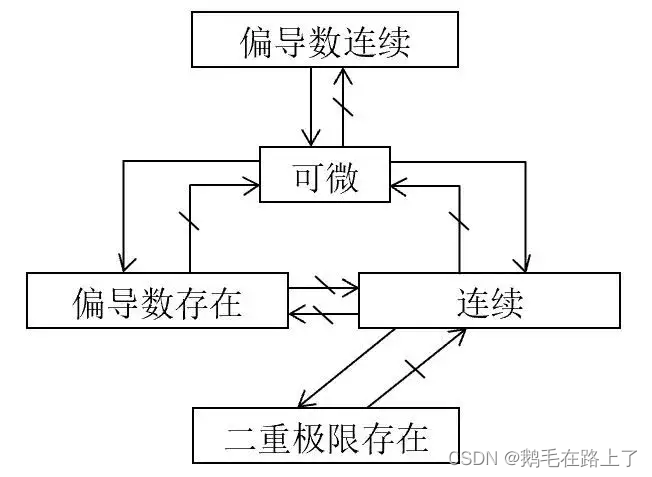
注意,以上关系图中均为单向箭头,即全是必要条件
多元函数求极限
夹逼准则用的比较多。
有界函数
无穷小量 = 无穷小量 重要极限
利用极坐标公式转换到一元函数
多元函数偏导数定义
对
对
多元函数可微的定义
函数
此处的根本定义如下:
其中,
而将其各部分展开得到的就是下面这个公式:
其中,可微的必要条件:
若
求解多元函数极值点

求解点到曲面的最短距离问题(最大值|最小值问题)
此类问题一般为给定条件下,求解最大或最小值问题。
其实无论是直接的点到曲面的距离,还是直线到曲面的距离,亦或者是曲面到曲面的距离。都可以使用下面的方法来解决。
此类问题统称为有限元极值问题。
通解为构造拉格朗日函数,找到其驻点,最后求解。
其中,
下面用例题说明:
例:880 P 43 T 6
求双曲线
首先是在双曲线上任意取一点
下面构造拉格朗日函数。
令
对
然后解上面方程组,得到驻点。
驻点分别为:
然后将驻点分别带入距离公式
NOTE
在上面进行计算的时候,我们将原条件
除了上面的距离问题,还有其他的一些问题,比如:当有限元问题中出现多个限制条件,那么就不一定是单一的
例如 880 P 43 T 8
微分方程
微分方程解的结构
#TODO
数列极限问题
在求数列极限的时候,如果是
不出意外的话,这个
然后就是写过程,首先是用数学归纳法证明有界性。
- 首项成立
- 假设第
项也成立 - 代入到条件中,证明第
项也成立。 - 得到结论
然后是证明单调性
利用后一项减前一项:
接下来就可以选择构造函数进行求导、使用数学归纳法,或者什么也不用,根据某些函数的性质、题目中的条件(大于 0 或者小于 0)即可得到证明。
NOTE
此外,如果是数列极限与积分相结合,首先考虑观察此积分是否能计算出来。如果不能计算出来,需要考虑积分中值定理或者放缩加夹逼
NOTE
在证明数列
常见泰勒公式
下面进行补充一个不是很常用的等价无穷小:
这个地方还是比较好用的,如果
下面是推导过程:
关键点在于换成幂指函数的形式,然后利用泰勒展开即可。
来一道综合泰勒公式缝合极限题:
 王海平
王海平